G12FCO -- Formal Computation
Lecture 12 -- Some more NP-complete problems
bottom of page
Now that we have one NP-complete problem, we can use that to find lots more.
The basic idea is to transform SAT [or, in due course, any other
NP-complete problem] to a new problem;
because the transformation is transitive, this will show that any
problem in NP can be transformed to our new problem, and so
that the new problem is also NP-complete.
We start with a trivial but useful new problem:
3SAT is NP-complete
3SAT is the restriction of SAT to the case where every
clause includes exactly three variables.
This regular structure makes it easier to transform than SAT.
- 3SAT is in NP [obvious, if only because it is
a subset of SAT].
- Given an arbitrary instance of SAT, we show how to
transform it into an instance of 3SAT.
Look in turn at each clause of the instance of SAT:
- If it has fewer than three variables, repeat a variable
as necessary;
e.g.
(a or not b) =>
(a or a or not b).
- If it has more than three variables, introduce a new
variable, and use it to split the clause into one with three
variables and another with one fewer variables [which can be
reduced the same way]:
e.g.
(a or not b or c
or not d or not e) =>
(a or not b or z)
and (not z or c
or not d or not e).
- The resulting formula can clearly be produced in time proportional
to the size of the instance, and is clearly satisfiable if and
only if the original formula was.
So
- SAT transf 3SAT.
Since SAT is NP-complete, so must be 3SAT.
QED.
Note which way round the proof goes.
To show that some new problem X is NP-complete, we have to choose
an arbitrary instance of a known NP-complete problem, such as
SAT [but we can now use 3SAT, and soon we'll be able to
use VC, HP, TS and other problems],
and show that that arbitrary instance can be transformed
in polynomial time into an instance of X.
This shows that [for example] SAT transf X, so that Y transf X
for an arbitrary problem Y in NP [because transformations
are transitive and because we have an intermediate `universal' problem],
and so that X is NP-complete.
This is the other way around from most of mathematics, where we would
prefer to start by relating an instance of the unknown problem to one
for an already-understood problem.
Also, don't forget always to show that X is in NP and that
the transformation is polynomial -- it is usually obvious enough, so that
you can just say `clearly ...'.
Vertex Cover is NP-complete
Vextex cover, or VC, is the network problem of determining
how many nodes you need to select to include at least one end of every edge.
We can turn it into a decision problem by asking whether this can be done
with so-many nodes -- then, if need be, we can turn it into a count by
homing in from the decision problem by using binary chop ["Can it be done
with 64 nodes? Yes, can it be done with 32 nodes? No, can it be done
with 48 nodes? ..."]
We can put the problem into more homely forms.
Referring back to our usual `roads and villages', we can ask which villages
need to have forts built in them so that every road has an associated fort.
Or we could ask how many rooms in a museum need to have a security man
posted in them so that every door is overlooked.
Or how many students need to be told something so that the entire class
will know before the next lecture.
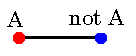 We choose to transform from 3SAT.
Given an arbitrary instance of 3SAT, we construct some roads and
villages to correspond.
For each variable, such as A, in the formula, we make two villages,
which we can think of as A and not A, with a road between them.
In order to cover this road, either A or not A will have to
have a fort;
I'm not going to give you enough forts for both villages, so you will have
to choose whether A is
We choose to transform from 3SAT.
Given an arbitrary instance of 3SAT, we construct some roads and
villages to correspond.
For each variable, such as A, in the formula, we make two villages,
which we can think of as A and not A, with a road between them.
In order to cover this road, either A or not A will have to
have a fort;
I'm not going to give you enough forts for both villages, so you will have
to choose whether A is true or false.
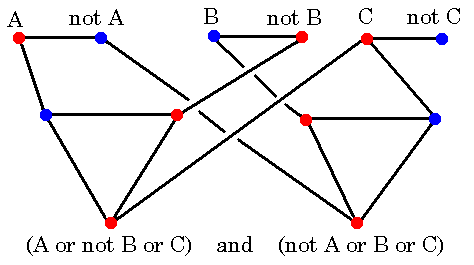 Now how about the clauses in the formula?
For each of these, we make three villages in a triangle with the roads
between them.
You will need two forts to cover these three roads;
I'm not going to give you a third fort, so each triangle will have to have
one village unguarded.
Now we join up each village in the triangle to the appropriate `variable';
see the diagram for an example.
Two of these new roads will be guarded by the two forts in the triangle,
but the third can't be, so must be guarded by a `variable' fort.
Now how about the clauses in the formula?
For each of these, we make three villages in a triangle with the roads
between them.
You will need two forts to cover these three roads;
I'm not going to give you a third fort, so each triangle will have to have
one village unguarded.
Now we join up each village in the triangle to the appropriate `variable';
see the diagram for an example.
Two of these new roads will be guarded by the two forts in the triangle,
but the third can't be, so must be guarded by a `variable' fort.
In other words, the formula is satisfiable if and only if there is an
assignment of forts to the variables such that every triangle has one
of its vertices connected to them.
So, this instance of 3SAT corresponds precisely to VC
for this network and for a number of forts equal to twice the number
of triangles plus the number of variables.
We can now complete our proof:
- VC is in NP, for in polynomial time we can `guess' a
collection of forts and check whether they overlook all the roads.
- 3SAT transf VC, by the above construction.
- But 3SAT is NP-complete;
hence so is VC.
QED
Hamiltonian Circuit is NP-complete
We sketch the proof;
for details, see the book by Papadimitriou.
There is a quite different proof in Garey and Johnson, based on a
transformation from VC.
We again work from 3SAT, transforming a formula into a network
which either does or does not have a Hamiltonian circuit.
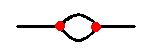 Again, there is a component for each variable.
This is very simple [see right];
in order to get between the two villages, you must choose either the
`high' road or the `low' road, so we can label one as A and the
other as not A.
For the clauses in the formula, we again use triangles.
Again, there is a component for each variable.
This is very simple [see right];
in order to get between the two villages, you must choose either the
`high' road or the `low' road, so we can label one as A and the
other as not A.
For the clauses in the formula, we again use triangles.
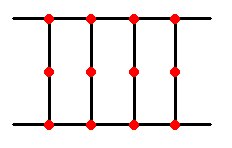 The `roads' in these are joined to the `variable' roads by the
construction shown to the left;
in order to tour round all these villages, you must either come in along
the top road, go down, up, down and up, and out along the top road again,
or else similarly from the bottom road.
So, if we make the top edge of this construction be either the high road
or the low road, as appropriate, of a suitable variable, and the bottom
edge be one side of a triangle, we can enforce that a Hamiltonian tour
includes either a suitable variable or the edge of a triangle.
For any clause that cannot be satisfied, all the corresponding
villages must be toured from the triangle, not from the variables,
and this will, so to speak, `disconnect' the triangle from
the rest of the tour.
Everything else is detail;
see Papadimitriou pp. 194-197 if you get stuck.
The `roads' in these are joined to the `variable' roads by the
construction shown to the left;
in order to tour round all these villages, you must either come in along
the top road, go down, up, down and up, and out along the top road again,
or else similarly from the bottom road.
So, if we make the top edge of this construction be either the high road
or the low road, as appropriate, of a suitable variable, and the bottom
edge be one side of a triangle, we can enforce that a Hamiltonian tour
includes either a suitable variable or the edge of a triangle.
For any clause that cannot be satisfied, all the corresponding
villages must be toured from the triangle, not from the variables,
and this will, so to speak, `disconnect' the triangle from
the rest of the tour.
Everything else is detail;
see Papadimitriou pp. 194-197 if you get stuck.
You might wonder how on earth anyone thinks of these proofs.
Basically, you need ingenuity, experience and luck.
But the main ideas are straightforward enough.
You start with a `sympathetic' known NP-complete problem, if possible
one whose structure seems to be cognate to the problem you are investigating.
Then you need to construct a suitable instance of your problem from an
arbitrary instance of the known problem.
This could be some sort of special case, or a simple identity;
in the more difficult cases, you will have to use what Garey and Johnson
call `component design' -- that is, each feature of the known problem
will map to a construction in the new problem.
In transformations from 3SAT, the components are the variables,
which must be true or false, and the clauses,
which must connect with three variables;
so the design must provide ways of enforcing choices and of connecting
clauses to variables.
Travelling Salesman Decision is NP-complete
Proof:
firstly, TS is in NP [obvious];
secondly, HC transf TS, as previously shown;
and thirdly, HC is NP-complete, as just shown, hence so
is TS.
top of page
 G12FCO home page.
G12FCO home page.
 Previous lecture.
Previous lecture.
 Next lecture.
Next lecture.
 Coursework 3 .
Coursework 3 .
Copyright © Dr A. N. Walker, 1996, 2016.
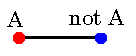 We choose to transform from 3SAT.
Given an arbitrary instance of 3SAT, we construct some roads and
villages to correspond.
For each variable, such as A, in the formula, we make two villages,
which we can think of as A and not A, with a road between them.
In order to cover this road, either A or not A will have to
have a fort;
I'm not going to give you enough forts for both villages, so you will have
to choose whether A is
We choose to transform from 3SAT.
Given an arbitrary instance of 3SAT, we construct some roads and
villages to correspond.
For each variable, such as A, in the formula, we make two villages,
which we can think of as A and not A, with a road between them.
In order to cover this road, either A or not A will have to
have a fort;
I'm not going to give you enough forts for both villages, so you will have
to choose whether A is  Now how about the clauses in the formula?
For each of these, we make three villages in a triangle with the roads
between them.
You will need two forts to cover these three roads;
I'm not going to give you a third fort, so each triangle will have to have
one village unguarded.
Now we join up each village in the triangle to the appropriate `variable';
see the diagram for an example.
Two of these new roads will be guarded by the two forts in the triangle,
but the third can't be, so must be guarded by a `variable' fort.
Now how about the clauses in the formula?
For each of these, we make three villages in a triangle with the roads
between them.
You will need two forts to cover these three roads;
I'm not going to give you a third fort, so each triangle will have to have
one village unguarded.
Now we join up each village in the triangle to the appropriate `variable';
see the diagram for an example.
Two of these new roads will be guarded by the two forts in the triangle,
but the third can't be, so must be guarded by a `variable' fort.
 Again, there is a component for each variable.
This is very simple [see right];
in order to get between the two villages, you must choose either the
`high' road or the `low' road, so we can label one as A and the
other as not A.
For the clauses in the formula, we again use triangles.
Again, there is a component for each variable.
This is very simple [see right];
in order to get between the two villages, you must choose either the
`high' road or the `low' road, so we can label one as A and the
other as not A.
For the clauses in the formula, we again use triangles.
 The `roads' in these are joined to the `variable' roads by the
construction shown to the left;
in order to tour round all these villages, you must either come in along
the top road, go down, up, down and up, and out along the top road again,
or else similarly from the bottom road.
So, if we make the top edge of this construction be either the high road
or the low road, as appropriate, of a suitable variable, and the bottom
edge be one side of a triangle, we can enforce that a Hamiltonian tour
includes either a suitable variable or the edge of a triangle.
For any clause that cannot be satisfied, all the corresponding
villages must be toured from the triangle, not from the variables,
and this will, so to speak, `disconnect' the triangle from
the rest of the tour.
Everything else is detail;
see Papadimitriou pp. 194-197 if you get stuck.
The `roads' in these are joined to the `variable' roads by the
construction shown to the left;
in order to tour round all these villages, you must either come in along
the top road, go down, up, down and up, and out along the top road again,
or else similarly from the bottom road.
So, if we make the top edge of this construction be either the high road
or the low road, as appropriate, of a suitable variable, and the bottom
edge be one side of a triangle, we can enforce that a Hamiltonian tour
includes either a suitable variable or the edge of a triangle.
For any clause that cannot be satisfied, all the corresponding
villages must be toured from the triangle, not from the variables,
and this will, so to speak, `disconnect' the triangle from
the rest of the tour.
Everything else is detail;
see Papadimitriou pp. 194-197 if you get stuck.