G12FCO -- Formal Computation
Lecture 15 -- What is a computer?
bottom of page
Computing Machines
Thus far, we have not really specified what we mean by a computer or
a computation.
For the rest of this module, we look more closely at this very
fundamental question.
Surprisingly many of the answers date back to the period before we
even had computers!
As this is not an engineering module, we are not primarily concerned
[and they certainly weren't in the 1930s and before!] with the actual
circuits, transistors, valves, string, sealing wax, silicon, paper or
magnetic tape, and other contraptions that go to make up a computer.
We are concerned only with the behaviour of these components.
More specifically, we assume that each component is a
`black box', which has some inputs and some outputs associated with it.
The inputs [0, 1 or more of them] come from other components or from
the outside world -- e.g. a temperature sensor,
or a photo-electric voltage representing `hole' or `no-hole' in
a punched paper tape, or a user typing something at a keyboard or
moving a mouse.
The outputs [1 or more] go to other components or to the outside world,
either as information written to a screen or other device or as a voltage
[or whatever] that drives some external device.
A component with no outputs is essentially useless;
one with no inputs may be used as, for example, a source
of clock pulses or of random numbers.
Since we are concerned with logical behaviour and not physical behaviour,
we assume that inputs, outputs, time, and other parameters of the system
are quantised.
That means that time proceeds in definite `ticks';
at each tick, our black box can inspect its inputs and will find
each of them in one of a number of definite `states',
will itself be in one of a number of definite states,
and will set each of its outputs to one of a number of definite states.
This idea is much more familiar to us today than it was to
mathematicians in the 1930s when these ideas were first
being discussed.
Many apparently continuous devices [photographs, telephone
conversations, gramophone records, handwriting] are routinely
handled by digital means today [television raster scans or CCD
arrays, computerised telephone exchanges, CDs, keyboards].
Early papers spend much time explaining how a continuous
function can be approximated by a sufficiently fine set of
discrete values.
Any device can then be characterised by a matrix.
Each row of this matrix corresponds to one of the internal states of
the device;
each column to one of the possible states of the inputs;
each entry to what happens to the device if it is in this state and
detects this input.
For deterministic machines, this entry will state what the next state
of the device will be, and what the output will be;
for probabilistic machines, it will have to include information about the
probabilities with which the consequent events occur.
At least in the simple case, this slightly unconventional matrix can be
replaced by two perfectly normal matrices, one for state, one for output.
Example:
A one-bit memory has two states:
0 [off] and 1 [on].
It has three inputs, each of which is either inactive [0] or
active [1]:
one to set the memory `on', one to clear it `off',
and one to read its contents.
There is one output, which is a copy of the memory if the
`read' input is active and is otherwise `off'.
This component can be described by the following pair of matrices:
| | next state | | | output
|
|
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111
| |
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111
|
| 0
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0
|
| 1
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1
|
[Assumes that if both `set' and `clear' inputs are active
simultaneously, then the status quo continues.]
See also the example below.
Note that it is unusual that there should be only 0s and 1s in
these matrices -- a more complicated component might have dozens
[or hundreds or billions] of states and possible outputs.
Notes:
- If several, or many, components are combined, the result is
another [usually much more complicated] component.
- Several things really don't matter about the inputs:
- It doesn't matter whether we think of several inputs,
each in one of several states, or a single `jumbo' input,
with many possible states [effectively, the Cartesian product
of the separate inputs].
- It doesn't matter what the states are `called', we might
just as well think of them as mapped onto a sufficiently
large range of integers [e.g. red = 0, green = 1,
blue = 2].
- If an input has many possible states, we can if we like think
of it instead as several binary inputs, each representing one
digit of the state number [so the number 37, binary 100101,
could be represented by 1, 0, 0, 1, 0, 1].
Converting between these representations is a simple
programming/logic/electronic task.
- If there are several binary inputs, it doesn't matter
whether these are presented in parallel along several
inputs or in series as successive values of a single input.
A simple component can convert between these representations.
Of course, a series presentation takes more ticks, so you
may have to run the components `faster' in order to get
the same results in the same time.
We shall make use of these freedoms to choose whichever
representation of the input is most convenient, rather than most
likely to occur in practice.
- Likewise for the output.
- If there is no input, or if it is constant, then after a number
of ticks not exceeding the total number of states the next state
must be one that has occurred before.
From this point on, a deterministic component must cycle through
the same sequence of states again and again.
Finite and isolated deterministic machines may have an initial
transient behaviour, but they must eventually enter a loop.
[For real computers, the time before this happens may be
extremely large.]
Finite and Infinite machines
`Infinite' here is a misnomer, though one that is hallowed by usage.
All computers are, of course, finite.
But there is a distinction to be made between computations that are
`bounded' in nature and those that are unbounded.
An interesting unbounded computation cannot be carried out by an
isolated deterministic computer, for, as we have just seen, such a
computer must eventually loop, and therefore its output will loop.
[OK for printing recurring decimals, not for much else!]
This may be irrelevant if your computer is not isolated [for we
expect the user to type different things at the keyboard, we expect
the temperature to vary, we expect incoming e-mail or Web pages to
change the way the computer behaves].
So, an interesting calculation needs an unbounded computer.
This may simply mean that the calculation has not yet hit the bounds
that the computer has;
but a more interesting way to make computers unbounded is to allow them
to expand as the calculation proceeds.
In real life, we can see this in action when the computer says
PLEASE PUT THE NEXT DISC INTO THE DRIVE, PRESS ANY KEY WHEN READY
TO PROCEED.
As long as we can supply new discs whenever needed, and recover old
ones upon request, a finite computer has been given an unbounded amount
of storage.
Note that as long as we keep the discs in order, then the computer can
ask for the next disc or the previous disc till the cows come home;
but it cannot in general ask for a specifically-numbered disc,
for in an unbounded calculation the number of the disc will eventually
become too large for the computer to store, even with the help of
the entire hard disc and the floppy drive.
Naturally, this is a theoretical rather than practical constraint!
Anyway, we now look briefly at what finite machines look like and
what they can and cannot do, and then we do likewise for unbounded
machines.
We start with an example of a model for finite machines that was
initially developed for a quite different purpose, just to show
that computers are not necessarily made of transistors and bits
and bytes.
McCulloch-Pitts cells
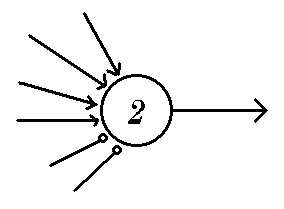 These were developed in 1943 [and so before anyone outside the
most secret recesses of intelligence agencies knew anything much
about real computers] by M & P as models of brain function.
A typical example is shown to the right.
This is meant to model a single brain cell, or neuron.
[There is no implication that brain cells really work like this --
M & P were rather looking for something that modelled the most important
aspects of neurons and that could be investigated to see what they
were capable of.]
Each cell has one output fibre -- the arrow to the right -- which, at each
tick, either `fires' or is quiet.
This fibre may later split;
each branch either eventually becomes an input fibre for some cell, or
else is a primary output [the `result' of some computation].
There are two sorts of input;
those coming in as arrows are `excitatory';
they tend to fire the cell.
Those coming in to little circles are `inhibitory';
the cell cannot fire while being inhibited.
Finally, each cell has a `threshold'.
After a tick, the output fibre fires if and only if
before the tick none of the inhibitory fibres
are firing and the number of excitatory inputs firing is at least
equal to the threshold.
So the example cell will fire as long as neither of the two bottom
input fibres is firing and at least two of the four upper fibres
are firing.
These were developed in 1943 [and so before anyone outside the
most secret recesses of intelligence agencies knew anything much
about real computers] by M & P as models of brain function.
A typical example is shown to the right.
This is meant to model a single brain cell, or neuron.
[There is no implication that brain cells really work like this --
M & P were rather looking for something that modelled the most important
aspects of neurons and that could be investigated to see what they
were capable of.]
Each cell has one output fibre -- the arrow to the right -- which, at each
tick, either `fires' or is quiet.
This fibre may later split;
each branch either eventually becomes an input fibre for some cell, or
else is a primary output [the `result' of some computation].
There are two sorts of input;
those coming in as arrows are `excitatory';
they tend to fire the cell.
Those coming in to little circles are `inhibitory';
the cell cannot fire while being inhibited.
Finally, each cell has a `threshold'.
After a tick, the output fibre fires if and only if
before the tick none of the inhibitory fibres
are firing and the number of excitatory inputs firing is at least
equal to the threshold.
So the example cell will fire as long as neither of the two bottom
input fibres is firing and at least two of the four upper fibres
are firing.
 A full discussion would take us too far afield, but the
examples left show that we can easily construct cells to emulate
logical and, or and not.
So it is easy to construct arbitrarily complicated logical functions,
and hence the whole of mathematics!
Well, more-or-less.
There is much more about all this in Minsky.
A full discussion would take us too far afield, but the
examples left show that we can easily construct cells to emulate
logical and, or and not.
So it is easy to construct arbitrarily complicated logical functions,
and hence the whole of mathematics!
Well, more-or-less.
There is much more about all this in Minsky.
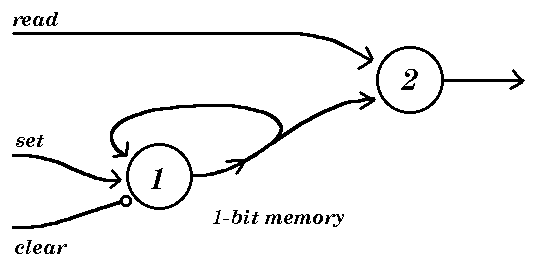 For a slightly more extended example, here is a single bit of memory.
The memory itself is the lower cell;
note the simple feedback loop which enables it to retain its state
of firing or quiet.
It will be switched on whenever the excitor fires, and
off whenever the inhibitor fires.
[Note that, in contrast to the matrix given above, if both inputs fire
simultaneously, the cell is switched off, not left as is.]
At every tick, the memory state is `copied' to the upper and-cell,
which therefore copies the memory to the output whenever [and only
when] the `read' fibre fires;
so a memory bank of these cells can be set or cleared in any combination,
and arbitrary subsets of them `read', emulating the real behaviour
of computer memory.
[However, there is an inherent delay;
the output fibre fires depending on the state of the memory cell
before the previous, not the current, tick.]
For a slightly more extended example, here is a single bit of memory.
The memory itself is the lower cell;
note the simple feedback loop which enables it to retain its state
of firing or quiet.
It will be switched on whenever the excitor fires, and
off whenever the inhibitor fires.
[Note that, in contrast to the matrix given above, if both inputs fire
simultaneously, the cell is switched off, not left as is.]
At every tick, the memory state is `copied' to the upper and-cell,
which therefore copies the memory to the output whenever [and only
when] the `read' fibre fires;
so a memory bank of these cells can be set or cleared in any combination,
and arbitrary subsets of them `read', emulating the real behaviour
of computer memory.
[However, there is an inherent delay;
the output fibre fires depending on the state of the memory cell
before the previous, not the current, tick.]
It would not be incredibly hard to build a neuron network that modelled
the behaviour of a real computer circuit.
Minsky shows that an arbitrary finite machine can be emulated by a
neuron network that uses only the and, or and not
cells previously shown.
top of page
 G12FCO home page.
G12FCO home page.
 Previous lecture.
Previous lecture.
 Next lecture.
Next lecture.
 Coursework 4 .
Coursework 4 .
Copyright © Dr A. N. Walker, 1996, 2016.
 A full discussion would take us too far afield, but the
examples left show that we can easily construct cells to emulate
logical and, or and not.
So it is easy to construct arbitrarily complicated logical functions,
and hence the whole of mathematics!
Well, more-or-less.
There is much more about all this in Minsky.
A full discussion would take us too far afield, but the
examples left show that we can easily construct cells to emulate
logical and, or and not.
So it is easy to construct arbitrarily complicated logical functions,
and hence the whole of mathematics!
Well, more-or-less.
There is much more about all this in Minsky.
 These were developed in 1943 [and so before anyone outside the
most secret recesses of intelligence agencies knew anything much
about real computers] by M & P as models of brain function.
A typical example is shown to the right.
This is meant to model a single brain cell, or neuron.
[There is no implication that brain cells really work like this --
M & P were rather looking for something that modelled the most important
aspects of neurons and that could be investigated to see what they
were capable of.]
Each cell has one output fibre -- the arrow to the right -- which, at each
tick, either `fires' or is quiet.
This fibre may later split;
each branch either eventually becomes an input fibre for some cell, or
else is a primary output [the `result' of some computation].
There are two sorts of input;
those coming in as arrows are `excitatory';
they tend to fire the cell.
Those coming in to little circles are `inhibitory';
the cell cannot fire while being inhibited.
Finally, each cell has a `threshold'.
After a tick, the output fibre fires if and only if
before the tick none of the inhibitory fibres
are firing and the number of excitatory inputs firing is at least
equal to the threshold.
So the example cell will fire as long as neither of the two bottom
input fibres is firing and at least two of the four upper fibres
are firing.
These were developed in 1943 [and so before anyone outside the
most secret recesses of intelligence agencies knew anything much
about real computers] by M & P as models of brain function.
A typical example is shown to the right.
This is meant to model a single brain cell, or neuron.
[There is no implication that brain cells really work like this --
M & P were rather looking for something that modelled the most important
aspects of neurons and that could be investigated to see what they
were capable of.]
Each cell has one output fibre -- the arrow to the right -- which, at each
tick, either `fires' or is quiet.
This fibre may later split;
each branch either eventually becomes an input fibre for some cell, or
else is a primary output [the `result' of some computation].
There are two sorts of input;
those coming in as arrows are `excitatory';
they tend to fire the cell.
Those coming in to little circles are `inhibitory';
the cell cannot fire while being inhibited.
Finally, each cell has a `threshold'.
After a tick, the output fibre fires if and only if
before the tick none of the inhibitory fibres
are firing and the number of excitatory inputs firing is at least
equal to the threshold.
So the example cell will fire as long as neither of the two bottom
input fibres is firing and at least two of the four upper fibres
are firing.
 For a slightly more extended example, here is a single bit of memory.
The memory itself is the lower cell;
note the simple feedback loop which enables it to retain its state
of firing or quiet.
It will be switched on whenever the excitor fires, and
off whenever the inhibitor fires.
[Note that, in contrast to the matrix given above, if both inputs fire
simultaneously, the cell is switched off, not left as is.]
At every tick, the memory state is `copied' to the upper and-cell,
which therefore copies the memory to the output whenever [and only
when] the `read' fibre fires;
so a memory bank of these cells can be set or cleared in any combination,
and arbitrary subsets of them `read', emulating the real behaviour
of computer memory.
[However, there is an inherent delay;
the output fibre fires depending on the state of the memory cell
before the previous, not the current, tick.]
For a slightly more extended example, here is a single bit of memory.
The memory itself is the lower cell;
note the simple feedback loop which enables it to retain its state
of firing or quiet.
It will be switched on whenever the excitor fires, and
off whenever the inhibitor fires.
[Note that, in contrast to the matrix given above, if both inputs fire
simultaneously, the cell is switched off, not left as is.]
At every tick, the memory state is `copied' to the upper and-cell,
which therefore copies the memory to the output whenever [and only
when] the `read' fibre fires;
so a memory bank of these cells can be set or cleared in any combination,
and arbitrary subsets of them `read', emulating the real behaviour
of computer memory.
[However, there is an inherent delay;
the output fibre fires depending on the state of the memory cell
before the previous, not the current, tick.]