G12FCO -- Formal Computation
Lecture 16 -- From finite to infinite
bottom of page
Powers and limitations of finite-state machines
Any inherently finite computation can be performed by some FSM
(and hence, for example, by a suitable network of McCulloch-Pitts cells).
Quite a lot of inherently unbounded computations can also be performed
this way.
For example, here is a `divide by 7' `machine';
for this, the `output' matrix comprises the quotient, and the `next state'
matrix is the remainder:
| | next state | output
|
| input: | 0 1 2 3 4 5 6 7 8 9 | 0 1 2 3 4 5 6 7 8 9
|
| 0 | 0 1 2 3 4 5 6 0 1 2 | 0 0 0 0 0 0 0 1 1 1
|
| 1 | 3 4 5 6 0 1 2 3 4 5 | 1 1 1 1 2 2 2 2 2 2
|
| 2 | 6 0 1 2 3 4 5 6 0 1 | 2 3 3 3 3 3 3 3 4 4
|
| 3 | 2 3 4 5 6 0 1 2 3 4 | 4 4 4 4 4 5 5 5 5 5
|
| 4 | 5 6 0 1 2 3 4 5 6 0 | 5 5 6 6 6 6 6 6 6 7
|
| 5 | 1 2 3 4 5 6 0 1 2 3 | 7 7 7 7 7 7 8 8 8 8
|
| 6 | 4 5 6 0 1 2 3 4 5 6 | 8 8 8 9 9 9 9 9 9 9
|
If you start this machine in state 0, and present it with an `infinite'
string of digits, it will output that string divided by seven.
Extending the machine to deal with several numbers separated by spaces, or
numbers that include decimal points, is left as an exercise.
However, here is perhaps the simplest `computation' that shows the limits
of an FSM:
The bracket-matching problem
When you include an arithmetic expression in a computer program, this will
in general include some [potentially nested] parentheses, as in
((a + b) * (c - d + 1) + 2)/(e + f).
Part of the task of a compiler or interpreter (the program that actually
turns your typing into machine code for the computer to obey) is to match
up the parentheses so as to determine the necessary arithmetic to evaluate
such expressions.
More generally, a typical computer language will also include brackets ([...]),
braces ({...}) and very possibly other forms of nestable `bracket', including
possibly constructs like `if...then...else...endif', but parentheses will be
enough for the present purpose.
There are two ways in which expressions may be malformed:
(a) if at any stage while reading the expression from left to right
there have been more right parentheses than left, as in `(a+b))';
or (b) if when the expression has been completely read there there have
been more left parentheses than right, as in `((a+b)'.
This is an easy programming exercise.
Essentially, you keep a count of the number of unmatched left parentheses;
this count is incremented every time you meet a left parenthesis, and
decremented when you meet a right parenthesis.
If ever the count goes negative, you have an unmatchable right parenthesis,
and if it is non-zero when you have completed reading the expression,
you have too many left parentheses.
So, why can this not be done by an FSM?
Because it cannot keep that count.
Suppose there is an FSM that can solve the bracket-matching problem,
and that has N states.
Feed it with left parentheses.
After no more than N steps, it must repeat a state;
suppose that after q steps, it repeats the state reached after
p steps;
that is, it is in the same state after reading (((...(((, whether
there are p or q parentheses in the string.
Now feed the FSM with p right parentheses and end the expression.
As the FSM is in the same state and is reading the same input, it will
continue to be in the same state.
If there had been p left parentheses, it would now signify that
the brackets matched correctly.
There were actually q, so they don't match.
So the FSM cannot give the correct answer in both cases.
This contradiction establishes the result.
This is a somewhat fraudulent proof [though no worse than most proofs
in mathematics!].
Firstly, in order to detect the repeated state, you need at least a
somewhat larger FSM than the one you're monitoring;
in other words, you can't build an FSM which busts bracket-matchers,
you have to wait until one is built that claims to match brackets,
and then you can build one that disproves the claim.
Secondly, even a single 32-bit word can hold enough states to do
bracket matching correctly as long as there are never more than
4293959295 unmatched left parentheses, which is enough for most
real programs, and if it isn't, a few more bits will suffice for
a universe-full of characters.
It gets much harder if there are several different sorts of bracket
to match!
Nevertheless, the idea is straightforward;
an FSM cannot, in principle, perform tasks that need an unbounded count,
as it will eventually run out of states.
These tasks include many simple mathematical operations, such as
multiplication, division [other than by a fixed constant and from
left to right], even addition from left to right [it's easy if you
present the numbers starting at the less significant end, but the
other way there is an unbounded carry in problems like
123456789... + 876543210...].
Beyond FSMs
If we want to build a more powerful mechanism than FSMs, then such a
mechanism has to have some unbounded part.
Many weird and wonderful mechanisms have been proposed, and exploring
their capabilities is a significant part of this part of mathematics.
They vary from an assortment of ideas based on real computers,
including stack machines [`push down automata'] which can save
information for later retrieval, or Petri nets [based on token-passing
mechanisms, rather like money, of which arbitrary amounts can be `saved'
in nodes rather like McCulloch-Pitts cells], through a whole spectrum
of which the other end is various forms of mathematical logic and
recursive function theory, passing through various sorts of re-write
system [rather like editors] and Conway's game of Life [much used in
screen-savers, but an interesting research topic in its own right].
Roughly in the middle of this spectrum, and by far the most theoretically
important unbounded mechanism is the so-called Turing machine.
This is not really a `machine' at all, but an abstraction, initially
intended to model the way mathematicians perform computations.
Turing machines
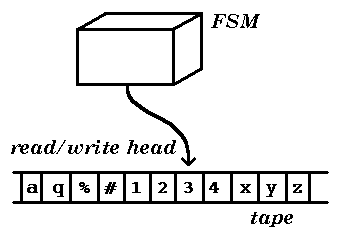 The basic idea is shown in the diagram.
The FSM is extended by having access, via a `read/write' head,
to an unbounded `tape' on which information can be stored.
This can be interpreted at several levels:
The basic idea is shown in the diagram.
The FSM is extended by having access, via a `read/write' head,
to an unbounded `tape' on which information can be stored.
This can be interpreted at several levels:
- The FSM could correspond to a mathematician with access to an
unlimited supply of paper.
As noted in the previous lecture, it doesn't matter whether
each `square' on the tape corresponds to a sheet of paper,
or to a square [big enough to hold one character] on a page
or squared paper or to a `pixel' in a TV picture of a page.
- The FSM could correspond to a computer with access to an
unlimited supply of floppy discs [or other medium].
- The FSM could correspond to the processing unit of a computer
with access to an unlimited main storage.
This is more problematical, as real main storages are not, even
in principle, unlimited [the machine architecture determines
the number of bits that can be used to address storage];
the distinction matters only if we in fact encounter the limits.
We assume that the FSM has a specified `initial' state in which to
begin the computation, and a specified `halt' state which, if reached,
signifies the end of the computation.
When we enter the halt state, we assume that there is some mechanism
[e.g. an encodingon the tape] whereby an external reader can
determine what the result of the computation has been.
The tape initially contains the specification of the particular
instance of the problem that the TM is designed to solve and is
otherwise supposed to be `blank' [if more than a finite part of
the tape is initially non-blank, then it could contain, in principle,
all the possible answers to all possible questions, and serve as a
super-oracle with unrealistic powers].
In each `cycle' of activity, the TM is expected to:
- read a character from the current position on the tape;
- change to a [possibly] different internal state;
- write a [possibly different] character to the current position
on the tape;
and
- move the read/write head left or right by one square [or
equivalently, move the tape right or left].
As with FSMs, much of the detail is irrelevant;
in each case, we can choose the version which is most convenient for
our purpose and know that the same results will apply to all TMs:
- The character set available for use on the tape could be ASCII
or binary or a whole `page' of information.
Transforming between these can be done within the FSM.
- You don't have to read from or write to the tape on each
cycle;
the FSM can ignore a character on input or write back the read
character on output.
Nor is the restriction to a single square of movement essential;
a state which moves, say, 7 squares right can be replaced by 7
intermediate steps each of which moves one square.
[There is no way within the FSM of specifying an unbounded move;
but of course you can use single steps to `search' the tape.]
- We don't need the tape to be unbounded at both ends.
We can use the mapping x -> 2x [if x >= 0],
x -> -1-2x [if x < 0] to `fold'
a doubly-unbounded tape into a singly-unbounded one.
A move left by a single square on the doubly-unbounded tape now
corresponds to a move by two squares left if you're on a non-zero
even-numbered square, by one square right if on the zero-numbered
square, and by two squares right if on an odd-numbered square;
this extra complication can be met either by maintaining more
states [and perhaps marking `end of tape'] or by extending the
character set to include this information.
- Similarly, it makes no difference to the abilities of the TM
[though, of course, it may make an enormous difference to the
efficiency with which it works] to have two tapes;
basically, you can interleave the tapes in a similar manner.
There is a complication in that you have to record in the
interleaved version where the read/write head on the `other'
tape is supposed to be, and you have to search for it when
you switch tapes.
More tapes, even unboundedly many of them [e.g. an
unbounded plane -- instead of linear -- tape] can be dealt with
in similar ways, but with more complex interleaving and arrangements
for the recording of where the heads are.
- Unwritten tape doesn't have to exist or be blank;
for example, it suffices if there is an `end-of-tape' marker
which can be pushed one square further away as necessary.
Bracket matching re-visited
A TM can easily solve the bracket-matching problem;
this will show that TMs are intrinsically more powerful than FSMs.
We assume that the tape initially looks rather like
...bb((()()))bb..., where b represents a blank square,
that the head is initially placed over the left-most parenthesis, and
that we start in state 1.
We describe the TM in similar fashion to an FSM, with the addition of
a matrix to indicate whether we move left [L] or right [R].
| | next state |
| output |
| direction
|
| input: | b | ( | ) | X |
| b | ( | ) | X |
| b | ( | ) | X
|
| state 1 | 3 | 1 | 2 | 1 | |
| ? | ( | X | X | |
| L | R | L | R
|
| state 2 | 4 | 1 | 4 | 2 | |
| f | X | i | X | |
| ? | R | ? | L
|
| state 3 | 4 | 4 | 4 | 3 | |
| s | f | i | X | |
| ? | ? | ? | L
|
| state 4 | ? | ? | ? | ? | |
| ? | ? | ? | ? | |
| ? | ? | ? | ?
|
Here, s is the success symbol, f the failure symbol,
and i represents an impossible combination, while
? represents an entry which is arbitrary or undefined.
Explanation:
State 1:
Scan to the right, looking for ) or blank.
State 2:
Scan to the left, looking for the ( to match the );
both will be replaced by X.
State 3:
Scan left looking for a blank;
no ) has been found.
State 4:
`Halt'.
Left as an exercise:
extending this example (a) to be able to restore the parentheses after
checking them;
or (b) to be able to start anywhere on the tape, not just over the
left-most parenthesis [so that first you must search -- in either
direction! -- for non-blank squares;
or (c) to be able to handle an arbitrary number of sequences [separated
by blanks] of more general brackets.
top of page
 G12FCO home page.
G12FCO home page.
 Previous lecture.
Previous lecture.
 Next lecture.
Next lecture.
 Coursework 4 .
Coursework 4 .
Copyright © Dr A. N. Walker, 1996, 2016.
 The basic idea is shown in the diagram.
The FSM is extended by having access, via a `read/write' head,
to an unbounded `tape' on which information can be stored.
This can be interpreted at several levels:
The basic idea is shown in the diagram.
The FSM is extended by having access, via a `read/write' head,
to an unbounded `tape' on which information can be stored.
This can be interpreted at several levels: