OK, something a bit different. You have a graph [mathematical, not engineering!], that is a collection of nodes and edges, so that each edge joins two of the nodes. Think, for example, of some villages, and the network of roads that connect them. In general, this network is `redundant', in the sense that there are usually several ways of getting from A to B. Equivalently, it usually has loops, meaning that you can start from A, go out along one road, and eventually come back to A by a different road. If you, somehow or other, break all the loops [e.g. by digging up some of the roads], then we finish with a [mathematical] forest. We shall assume that the network is connected, so that you can get from any village to any other [this is not the case in general -- some of the villages might be on islands or otherwise isolated]; in this case, the forest reduces to a single [mathematical] tree.
Suppose every road has an associated length. This is not necessarily the ordinary geometric length; it could be any measure associated with the road, such as the travel time along it, or the beauty of the scenery, or the number of pubs, or the cost to Diamond Cable of digging up the road to provide cable connexions between the villages. We can then ask -- `What is the shortest tree that connects all the villages?' -- the minimum spanning tree [MST]. [This question makes more sense for some measures than others!]
There are several ways to tackle this problem. One of the most natural is to construct the MST, village by village. As usual, we consider the state of affairs part-way through this process. We start with no roads known to be part of the MST, and we finish with all the villages connected by the designated roads. So the intermediate state will have some roads known [or at least strongly expected] to be part of the MST, and some villages connected by these roads. Will these roads be joined up? We don't know this for sure, but it would be nice; so let's see if we can make it work.
The intermediate configuration is, then, something like the
diagram.
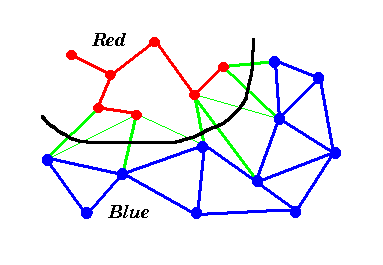We have some villages and roads that are part of the MST;
we colour these red.
Some villages are not yet connected up;
we colour these blue.
We also colour blue the roads that connect blue villages.
Roads between red villages that are not part of the MST
can be ignored/deleted.
There are also some roads between red and blue villages;
we colour these green.
The green roads form a `frontier' between the red and blue villages,
as shown by the black line.
To make progress, we must turn one of the blue villages red. If it is to maintain the connectedness of the tree, the chosen village must be the blue end of one of the green roads. Which green road? The shortest! It is intuitively obvious that the shortest would be a very good one to try; but we can easily prove that it really does work. For, suppose that this road is never chosen. Then when we complete the MST, it will nevertheless be possible to get between the two corresponding villages, and this route must include some other green road [for otherwise we can't ever get from a red village to a blue one]. If we now add in our shortest green edge, this will complete a loop; and deleting the other green road will leave everything connected but by a tree which is no longer [and indeed is shorter unless the green roads were of equal length]. So, we can select [one of] the shortest green roads and be sure that this can be part of an MST.
We can now sketch the algorithm.
[initialise] choose a village, colour it red, colour all its roads green, colour all other villages and roads blue. [loop] while there are any blue villages, find the shortest green road, colour it red, colour its blue village red, delete all the green roads from the newly-red village, and colour green all its blue roads.The `invariant' is essentially the given diagram; the red roads are part of the MST, red roads join red villages, etc. Every time around the loop, one blue village turns red, so this must terminate with the MST complete. We cannot prematurely run out of green roads, as the villages are connected.
Turning this into a computer program is a non-trivial exercise. You would have to decide how to represent the diagram, presumably with arrays describing the villages, roads, colours, etc. An implementation will also have to decide which village to choose first and how to break ties. None of this is difficult, it's just time-consuming.Have we now completed the MST problem? By no means! Suppose there are N villages. How much work will we have to do? There may be as many as N(N-1)/2 roads [not usually for real networks of roads in two dimensions]. Most of the roads start out blue, change to green and then change to red or disappear; this is more work than changing the villages, so the time taken for updating all the arrays will be O(N^2). But this work in turn is upstaged by the work of finding the shortest green road. In the worst case, there may be N^2/4 green roads [when there are N/2 red villages each joined to the same number of blue villages], so the work required to find the shortest of these roads each time round the loop may be O(N^2), and it is not hard to see that the total work may therefore be O(N^3).
Can we do better? Yes, because most of the green roads are the same each time, and we can make use of this to reduce the work. The trick is to note that of all the green roads joining a particular blue village to red villages, only one can be currently the shortest. The others can be discarded; they will never be the shortest overall green road. [A blue village can only be joined to a red village once; a red village can become joined to lots of blue villages, so care is needed!] So there need never be more than N green roads, and the total work of finding shortest green roads is O(N^2).
In the diagram, the discarded green roads are shown thinner. The computing `trick' is that whenever you should turn a road green, you compare it with the current green road from its blue end, discard it if longer, else the current one.
Is this the end of the story? By no means! This algorithm is known as Prim's algorithm. A quite different approach is Kruskal's greedy algorithm. In this, the edges are first sorted, then looked at one by one starting with the shortest. If the edge connects two villages which were previously unconnected, then it is part of the MST; if they are already connected, then the edge is discarded. Part-way through the algorithm, we have a forest, the trees of which gradually become connected. Kruskal's algorithm is better if there are relatively few edges and if the longest edge in the MST is relatively short; Prim's if the network is dense or if some villages are quite isolated.
G12FCO home page.
Previous lecture.
Next lecture.
Problem Class 2.