G12FCO -- Formal Computation

Problem Class 5 -- Machines -- solutions

Note: You weren't expected to complete these solutions within the problem class! As usual, the real point is the `Aha!' of getting the essentials correct, and the fine detail is time-consuming but necessary in the real world, but less important in class. I've given most of the fine detail here so that you can check your solutions against mine.

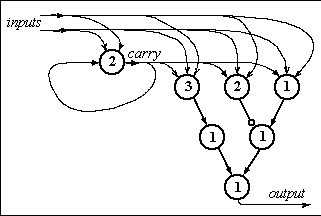
McCulloch-Pitts binary adder: There are quite a few possible solutions. The diagram shows one. The carry cell fires if and only if at least two of the input fibres and the previous carry fire. The output fibre should now fire if an odd number of the inputs and previous carry fire. So the next three cells pick up whether at least 3, at least 2 and at least 1 of them fire; the number is odd if either 3 or (1 but not 2) fire. Evaluating `1 but not 2' takes a tick, so we put a delay into the output from 3 before `or'ing the results. You can save a tick by splitting the three fibres into all eight possible cases, but then the diagram gets very messy.
Turing-machine binary adder: Let us develop this stage by stage. The first step is, as usual, to decide what the tape should look like part-way through the calculation. We will need three numbers, the [partial] addends and their [partial] sum, and perhaps some punctuation. We can save on punctuation by using a different alphabet for the middle number, say using a and b for 0 and 1, respectively. We're already using the + symbol, so we can continue to use this as an `ignore' symbol. So a typical intermediate state could be, say, X1010+++babba010X, meaning that we still have to add 1010 to babba [= 10110], with 010 being the `result so far'.
Now what? Well, we must scan left to pick up the rightmost digit [here 0] of the left operand. If there isn't one [we find X], then we've essentially finished, and just need to tidy up. If the digit is zero, then we replace it by +, to say we've used this digit, then scan right until we find the start of the answer [1, or X if this is the first digit], go back a place, replacing a or b by 0 or 1, and treating + as a [in case we've exhausted the right operand]; then start again. If the digit is one, then the scan right is the same, but the replacement is more complicated. We have to add one to the right operand; so we replace a by 1, but b by 0 and `carry one'.
So, there are three `phases'; convert to the initial `intermediate state', process all the digits [as above], and tidy up. Tidying up is left as an exercise, but we can expand the other phases:
State 0: [start, phase 1] Scan right, until we find the + [state 1]
State 1: Scan right, replacing 0, 1 by a b, until we find X [state 2]
State 2: [phase 2, start of main loop] Scan left. If we find X, we're done [tidy up, state 8]. On finding 0, enter state 3; or on finding 1 enter state 5
State 3: Scan right, looking for 0, 1 or X [state 4]
State 4: [add 0] Replace letter by digit, as described above, then state 2
State 5: As state 3, but then enter state 6
State 6: [add 1] Replace a or + by 1 and enter state 2, or replace b by 0 and enter state 7
State 7: [carry 1] Go left, replacing a by b and enter state 2, or replacing b by a [staying in state 7]
States 8, 9, ...: [tidy up, phase 3] Left as an exercise!
Here is the set of matrices for the first two phases [? indicates an impossible or arbitrary entry]:
```
          next state   output symbol   direction
   input  0 1 a b + X   0 1 a b + X   0 1 a b + X
state 0   0 0 ? ? 1 ?   0 1 ? ? + ?   R R ? ? R ?
      1   1 1 ? ? ? 2   a b ? ? ? X   R R ? ? ? L
      2   3 5 2 2 2 8   + + a b + X   R R L L L L
      3   4 4 3 3 3 4   0 1 a b + X   L L R R R L
      4   ? ? 2 2 2 ?   ? ? 0 1 0 ?   ? ? L L L ?
      5   6 6 5 5 5 6   0 1 a b + X   L L R R R L
      6   ? ? 2 7 2 ?   ? ? 1 0 1 ?   ? ? L L L ?
      7   ? ? 2 7 2 ?   ? ? b a b ?   ? ? L L L ?
      8   left as exercise!
```
Blank-to-blank TM: If we could solve this, we would be able to solve the blank-tape halting problem, and hence the halting problem. Given an instance of the BTHP, firstly re-write it so that the role of a blank square is everywhere replaced by using instead a new symbol, say X; secondly, add some new states so that whenever a blank is read, it is first replaced by an X; thirdly, replace any halt states by new states in which we first search left for a blank, then scan right replacing all symbols by blanks until we reach another blank. The first two steps mean that the revised machine behaves exactly like the first, except that everywhere it has visited is non-blank [every blank having been replaced by an X]. So its tape is always non-blank [after the first tick], unless and until the original machine would have halted, at which point the revised machine erases its tape. So the revised machine again has a blank tape if and only if the original machine halts, and thus if we could solve the BtB problem, we could solve the BTHP; but we can't, hence the result.

top of page

G12FCO home page. border=0

Previous discussion. border=0

Problem class.