G13CS3 -- Mathematical Aspects of Computing

Examples of McCulloch-Pitts cells

Example of [fairly random] network

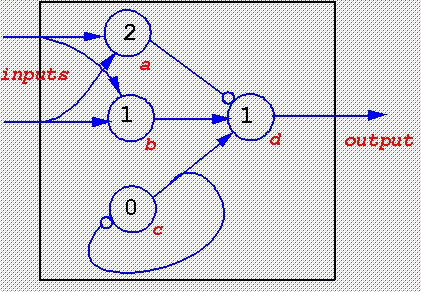
Corresponding description in form of matrices:

			    next state		  output
current state	input:	 00   01   10	11	00 01 10 11

  0 0 0 0		0010 0110 0110 1110	 0  0  0  0
  0 0 0 1		0010 0110 0110 1110	 1  1  1  1
  0 0 1 0		0001 0101 0101 1101	 0  0  0  0
  0 0 1 1		0001 0101 0101 1101	 1  1  1  1
  0 1 0 0		0011 0111 0111 1111	 0  0  0  0
    ...			 ...			  ...
    ...			 ...			  ...
  1 1 1 1		0000 0100 0100 1100	 1  1  1  1

Serial to parallel converter

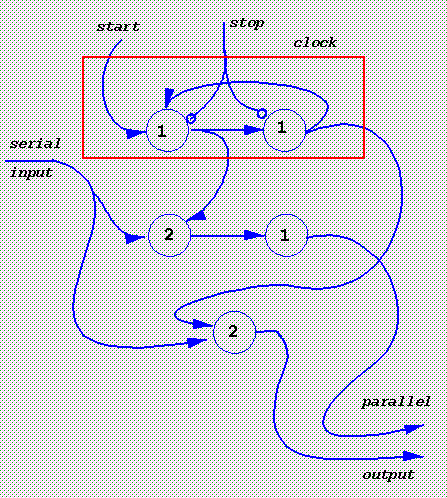
The `clock' can, of course, be extended to an arbitrary length of cycle. Note that the parallel output only fires on alternate `ticks'. This is inevitable. A parallel to serial converter is left as an exercise; correspondingly, this can only be done every so-many ticks.

Reduction of arbitrary FSM to M-P network

Reduction of complicated cells to simple ones

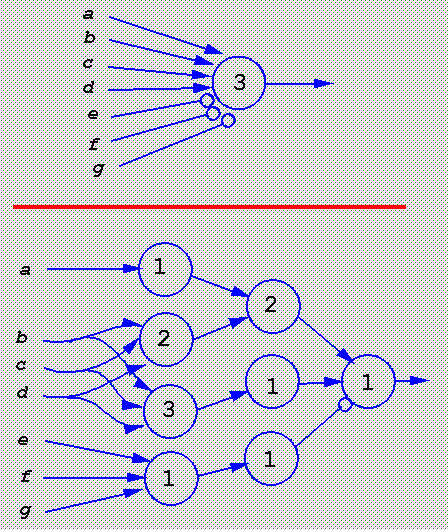
Note that although these two networks behave `logically' in the same way, the output from the lower is delayed by two ticks from that for the upper. The more complicated cells in the lower network can be replaced in the same way [at the expense of more delays], showing, ultimately, that only `and', `delay' and the rightmost cell of the lower network are needed. This cell in turn can be replaced by feeding the top two inputs into an `or' cell, the bottom one into a `not' cell, and `and'ing the results, while the `delay' is merely the `and' [or `or'] of two copies of its input; this shows that `and', `or' and `not' are `universal'. So too must be any collection of cells from which `and', `or' and `not' can be made up [more details in Minsky].