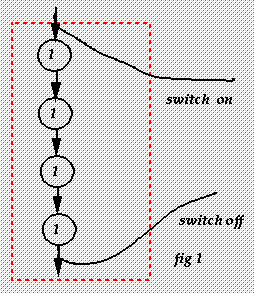
The basic component is the delay, shown in fig 1;
as shown it switches something on, then off again four ticks later,
clearly the number of ticks can be altered at whim.
Equally clearly, we can stack up several of these, or else
have a much longer delay with on and off fibres in several places,
as we prefer.
If we feed the last one back into the first, then we have a
repeating cycle.
Most of the Pelican crossing is now routine.
The flashing green man can either be controlled by a delay which
switches the man on and off repeatedly by brute force, or
by switching on, and later off, a flasher unit
[a loop of size two from which you alternately
switch on and off the green man].
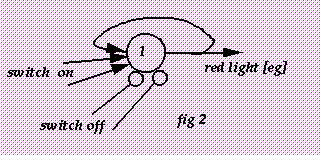
The switches themselves follow the model shown in fig 2.
This leaves two problems:
how to keep the lights on green for an arbitrarily long time
[until the button is pressed];
and how to use the button.
The first is easy; the green phase tails off into a switch, also like fig 2, so that once it fires, it keeps firing until switched off. This cell should not keep on starting the next [amber] phase, so the amber phase should have as its top cell one with threshold 2, rather than one, so that it starts only when it also receives another signal [from the input button, essentially]; either this other signal or the top cell of the amber phase should then switch off the green phase and the green light.
The second is now also easy. Have another switch to indicate that the halt button has been fired; that is, the input fibre is a `switch on' fibre for the halt switch. This switch will be tapped off for a switch on for the amber phase; as noted above, this will be ineffective until the green switch also fires. The halt switch should eventually be switched off. If you do this from the end of the steady green man, then pressing the halt button is ignored if you do it while the crossing is already in your favour, but the pressing is stored if you do it at or after the start of the flashing. It is then ignored until the green switch is activated, which is exactly the desired behaviour.
Everything else is now routine. One thing to watch out for: make sure that the start of the amber phase kills everything else in sight, otherwise it is easy to get the amber phase started twice on successive ticks, which is not good [though it doesn't really matter if things get switched on and off twice except for the flasher unit]. Real Pelican crossings [and other traffic lights, etc.] are more like this than you might suppose!
- Cannot.
Basically, trying to match palindromes like
aaaabaaaa is the same as the bracket-matching
problem, and a very similar proof works;
you have no way of keeping track of a proposed match.
A TM for this is fairly easy.
In state 0 [initial], scan left until you hit a blank,
then go right in state 1.
In state 1, if you find a blank, halt -- success;
otherwise, if you find X, enter state X1, if a Y state Y1,
etc., repeated over the alphabet, and write a blank,
and move right.
In state X1, if you read a blank, enter state X2 and move
left; if an X, stay in state X1, if any other character
enter state X3, in each case writing back what you have read
and moving right.
In state X2, write a blank [regardless of input], move left,
and enter state 0.
In state X3, if you read a blank, halt -- fail;
otherwise this is exactly like state X1.
Repeat over all characters.
Basically, we are trying to blank off the outermost pair
of characters;
if they don't agree, we fail, but if we blank off everything
then we succeed.
There is a palindrome detector running as a demo [along with
various busy beavers!] at
Suzanne Skinner's web site at Ohio
[you need a Java-enabled browser].
- OK.
The FSM can keep track of the remainder after the
number so far is divided by 4;
we succeed if we are in state 0 on reaching a non-digit.
For example, if we're in state 1 and read an 8, then we
enter state 2 [= remainder when 18 is divided by 4].
- Not possible.
No matter what order the numbers are presented in, there
will be more possible intermediate results than the
number of states can cope with.
Minsky, p125, section 6.1.4, gives a 4-state unary
multiplier -- the basic idea is to cross off one bit
of one operand and copy the other until the first operand
becomes empty.
For a demo, the
Buena Vista TM demo [programmed by Ken Schweller]
includes a `multiply' example
[it's an option in the menu next to the `load' button],
but you need to have a Java-capable browser.
No doubt there are others around the Net!
Andrew Hodges has some references to downloadable
TM simulators.
- OK, possibly surprisingly. If you know about regular expressions, or lexical analysis, then the fact that you can write numbers as REs or as lexemes establishes this fact. Otherwise, the basic idea is that a number consists of: (i) An optional sign, followed by an optional integer, followed by an optional decimal part, followed by an optional exponent. Not all the last three parts can be missing, so you have to write out the various possible cases separately. You know to start looking for the exponent, for example, when you hit an `e'. All this where (ii) an integer consists of a sequence of digits, (iii) a decimal part consists of `.' followed [if you like, optionally] by an integer, and (iv) an exponent part consists of `e' followed by an optional sign followed by an integer [not optional!]. From there it's easy.