The Analysis of Games

Before we look at games in general, I want to show you one game in particular as an example, which will help to orientate and motivate quite a lot of the later discussion.

Domineering

Let's play a game. This fairly simple game is called Domineering. You are given a squared board, which can be any size, such as a 4x6 or 5x7 rectangle. You are also given a supply of dominoes, each of the right size to cover just two of the squares. 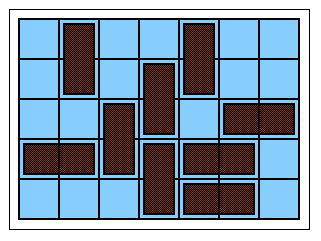There are two players, who take turns to place a domino on the board in such a way as to cover two adjacent squares; one player places the domino to cover two horizontally [or east-west] adjacent squares, the other to cover two vertically [or north-south] adjacent squares. No domino is later moved, or captured, or itself covered. So, after a while, the board may look like this example. As you keep playing, the board fills up, and eventually one of the players cannot place a domino; that player is the loser. [This is the most usual rule for winning or losing games: dum spiro spero, or `while there's life, there's hope'; as long as you keep moving, you survive, and you lose when you cannot move.]

If you have not seen Domineering before, then I suggest that you take time out to play a few games, to get the feel of how it works, before you read further. You don't need the dominoes if you just draw a board, and cross off or draw a line through the squares covered.

Now, how shall we analyse this game? Preferably not by brute force: there are several million million possible games on the 5x7 board. A computer could run through those in a reasonable time -- a few weeks -- but the time taken would then go up rapidly if we looked at larger boards. [On the other hand, by the time we reach a position such as that shown, there is much less work to do, and a computer could very easily analyse that -- the difficulties come from the early stages, when both players have a wide choice.] There are ways of making the `run through' much more efficient, as we shall see. But it is also important to make use of intelligence to simplify the task.

The first observation is that the history of how a square 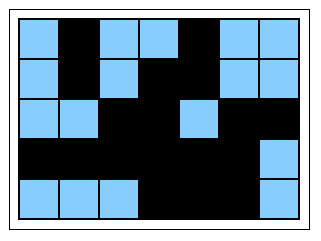became covered is [in this game!] unimportant; all that matters is which squares are covered, and which still open. So the previous example might just as well have been drawn like this:

Next, we note that the black squares play no further part at all in the game. so we might as well snip them away. When we do this, we get several separate parts, and it doesn't really matter where these are, we can move them around as long as we don't change their orientation and as long as we don't move them together in such a way to to make up an adjacent pair of squares from two separate pieces [which would create an extra move for one side]. The technical word for this separation is `disjunction'; our example position is the `disjunctive sum' of various smaller positions, as shown in the next figure:

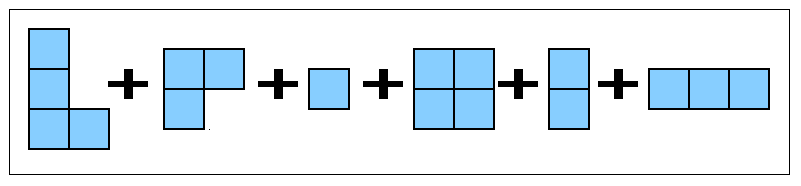
So, we are motivated to evaluate small positions, and to work out an `arithmetic' whereby we can `add' the resulting values. Some of this is remarkably easy, and quite intuitive; some of it is a little trickier, but shows a surprising relation between games and numbers; some of it shows that that relation should not be pushed too far, or alternatively that some number-like things are rather exotic. We can build up a table:

	This is an easy position; there are no moves at all in it. This is an example of the zero game, or null game, which we write 0. The zero game, in which nothing at all happens, is as important to game theory as the zero number is to arithmetic. Whoever is to move first in this position loses. We can discard isolated squares from a Domineering game; they make no difference at all to the play or the outcome.
	This is almost as easy. One player has exactly one move, the other player has none. This position represents a `free' move to the player of the horizontal dominoes. Moves are the `unit of currency' in games, so this position is called 1.
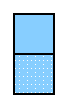
	This is a free move to the other player. So this is -1. Does this make sense? Yes, because 1 and -1 cancel out; they will have no influence on the outcome of the game, as they represent exactly one move to each side. In this sense, 1 + (-1) = 0, The players might just as well agree to discard matching pairs rather than play them out. Indeed, it's not hard to see that any disjunctive part of a game of Domineering can be cancelled against a similar shape that is rotated by a right angle -- every move in one part can be matched by a corresponding move in the other. Similarly, a strip of three horizontal squares is also 1, a strip of four or five is 2, and so on, and vertical strips similarly. You can then verify that 2 - 2 = 0 [shorthand for 2 + (-2) = 0], that 2 + 2 = 4 [in other words, that two strips of length four can be replaced by one of length eight without affecting the outcome of the game], and so on. Everything that you learned about adding and subtracting whole numbers in `traditional' mathematics might just as well have been learned by playing Domineering! Note that in a long strip, you only get the maximum number of moves if you play sensibly. Eg, in a strip of length 10, you can squeeze five dominoes by packing them together, or you can run out after only three if you [stupidly] leave gaps. This topic will be discussed later; for the time being, we just assume sensible play.
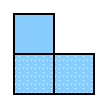
	This is one move for whoever gets to it first. Whoever uses it will leave nothing for the other side, and if you don't use it, your opponent will. This position is called *, or `star'. Note that if we turn * round, we get the same position, effectively, back again; so * is its own negative, and two stars cancel. As an equation, * = -*, or * + * = 0. But * is not 0, so something weird is going on.
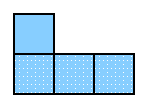
	This gets a little more complicated, as there may be one move or two. If the horizontal player gets to it first, then the move into the corner kills it; if the vertical player, then the other player will still have a move left over. So this position is good for horizontals, better than nothing, but not as good as a whole spare move [as there may be a move each]. What do we know that's better than 0, worse then 1? Yes, this position is called ½, or half. It is worth exactly half a horizontal free move. We confirm this by looking at the combination ½ + ½ - 1. The best move for each side is into the corner of a half, and as there are two halves, each side will get one of them, no matter who plays first. So after one move by each side, we reach 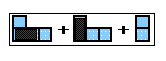, leaving just one more move each, cancelling out to zero. So the combination was worth exactly two moves to each side, and also cancels out, having no overall effect on the game, so ½ + ½ - 1 = 0 in games just as in ordinary arithmetic. If you get two halves and a -1 as disjunctive parts of a game of Domineering, you might as well agree with your opponent to throw them away, just as you might agree about two stars or about 1 and -1. You could, it will emerge, have learned about fractions just as well by playing games as by the more traditional school methods.
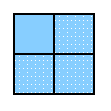
	Here is another position that, because of the symmetry, is its own negative, so that two of them cancel, and yet this is not the zero game. Whoever plays first creates a free move -- play a horizontal move, and there is a horizontal move left, or a vertical move and a vertical move is left. This is called ±1. It's a `hot' position -- if you have a chance to play in it, but don't, then your opponent gets the free move instead of you, so there is an effective `swing' of two moves, which is quite an incentive to play here. By contrast, the free moves of 1 or ½ are `cold'; when you play them, you use them up, so you prefer to leave them, and play the hot positions first.
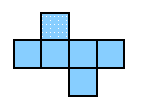
	One last curiosity. Here we have two stars wedged together to give an extra horizontal move. That move, playing across the middle, kills the rest of the position, leaving four separate squares. On the other hand, a vertical move leaves a star, with a horizontal move to come. So this is a good position to be playing horizontally, better than nothing, just like half; it's called ^ or up. How good is up? Well, not that good at all, really. It's infinitesimal. If there are a million of these, and one measly free vertical move, then it's still a vertical win. You just go from up to up, playing wherever you can, and not using your free move. As long as any ups are left, there will be horizontal moves in them; but also vertical moves, so you are never forced to use up your free move. Only when all the ups have gone do you have to play your free move; but then there are no horizontal moves left to play, and you win. Up is not a number, not even an infinitesimal number [and we shall find such beasties in game theory], worse than that, it's infinitesimal compared with even infinitesimal numbers, but it is positively better than nothing. You might think that bizarre enough, but up is still quite big compared with some other games. For example, the game which is similarly obtained by wedging together two ±1s into a 2x4 rectangle is infinitesimal compared with up, as we shall see in due course.

You might think that we've gone to a lot of trouble to give names to positions in this quite obscure game. The reason is that the same positions occur in the late stages of all sorts of games -- even, on occasion, chess. If there are only one or two moves to go to the end of the game. then there are not that many ways it can happen, so the same patterns come up again and again, and it helps to be able to recognise them and combine them with other simple games.

Some of the other features that we've looked at -- the relations between games and numbers [whole numbers, fractions, and others], teensy-weensy games, huge games, symmetry, cancellation, disjunction, temperature -- also come up again and again, motivating abstract studies of how they behave.

top of page