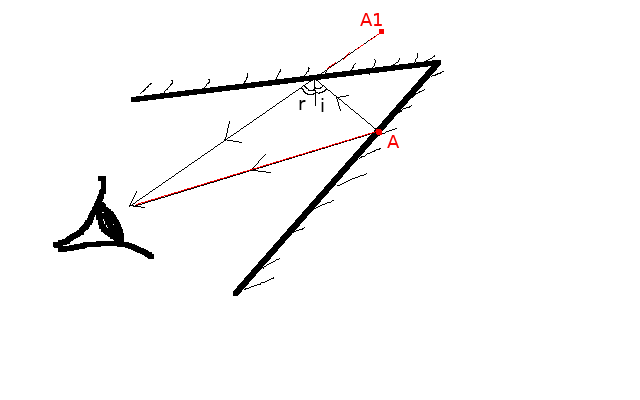
So, if A is in the real image, light coming to your eye directly comes on the red path. In addition, there will be light coming to your eye having bounced off the other mirror just once. Think of perfect billiard-ball bounces -- the angle of incidence, i, and the angle of reflection, r, are the same. [Aside: Angles i and r are traditionally measured from the perpendicular, as here, although unless your mirror is curved it makes little difference as the angles from the mirror are also equal.] This once-reflected light will look as if it is coming from point A1.

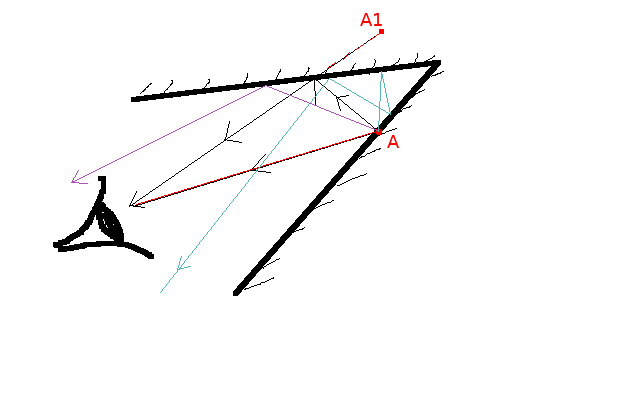
Despite bouncing around, most rays of light coming from this part of the image miss your eye and won't contribute to what you see. The rays that come in the direction of your eye will have to start out in directions that combine with the geometry in such a way that their succession of perfect bounces from the mirrors ends up sending the ray in exactly the right direction to reach your eye from the final bounce point. That final angle of the ray into your eye and the length of its total path will then fix the position of the apparent image you see from that ray. It is this that selects the particular collection of apparent images that you see. There may be only a few rays that start at point A and after bouncing around actually reach your eye. For each of these rays, you will see an apparent image of A. So you may see A, and A1, A2, ...

Depending on the angle between the mirrors, there can be various numbers of apparent images. It turns out that if the angle between the mirrors is 60 degrees, for instance, you will see six different images formed because along with the direct viewing path there are five different bouncing paths (all with equal angles of incidence and reflection at each bounce) that will reach your eye. If the angle between your mirrors is very small, there will be much more bouncing going on and you will see a much larger number of apparent images -- near parallel mirrors appear to show repeated images going off to infinity.

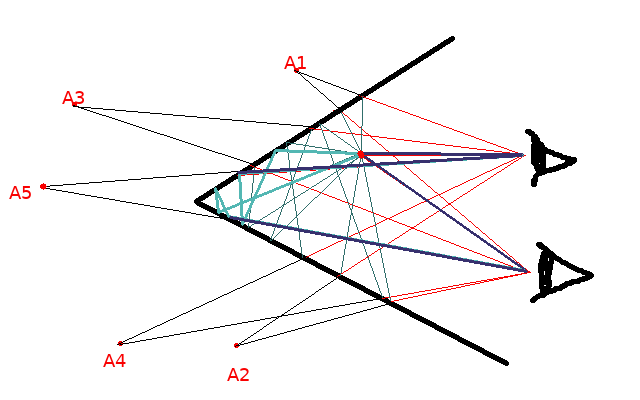
The schematic diagram above shows the rays reaching two different viewing positions from the red dot between two mirrors with a 60 degree angle between them. In this diagram I have drawn the red dot away from the mirrors for clarity. As well as seeing the dot directly, you will see that there are five apparent images A1, A2, A3, A4 and A5 resulting from rays that bounce off the mirrors 1, 1, 2, 2, and 3 times before reaching the eye. All viewing positions agree on the position of the apparent images, resulting in a powerful illusion.

Before closing, I should perhaps apologise for the sketchy nature of my diagrams. I hope you will also forgive me for not showing the light rays being bent through the lens of your eye and landing on your retina!

There is, of course, plenty of further material on the web about kaleidoscopes, including some about modern kaleidoscopes with unusual geometries that give amazing visual effects. If you search for 3D kaleidoscopes, you will probably come across some of these. [Here are some YouTube videos you might like: dodecahedron kaleidoscope, tapered kaleidoscope, tapered translucent kaleidoscope, ; Peek-a-Box Kaleidoscope.] Enjoy!